Toroidal Snarks and such

What is a graph?

Informal definition: A graph is a collection of dots that are connected in various ways by a bunch of lines. They're often used to represent networks. We call the dots vertices and the lines edges.

More-technical definition: A graph is a set of vertices, V, together with a set of edges E, where elements of E are unordered pairs of elements of V. We usually refer to these sets as V(G) and E(G) for a particular graph G.

Examples: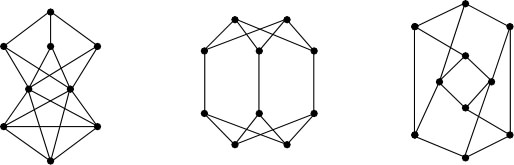

For further information... see the mathworld Graph page and this mathworld classroom article, and check out friendly books such as Richard Trudeau's Dots and Lines (okay, the current title is Introduction to Graph Theory but the old name was more indicative of the flavor of the book; it's readable by people who know no mathematics) or Chartrand/Zhang's A First Course in Graph Theory.

What is a surface?

Informal definition: A surface is a two-dimensional object without edges or corners, like shrink-wrap, the skin on cooked milk, the glaze on a doughnut, or a balloon, only infinitely thinner.

More-technical definition: A surface is a smooth compact 2-manifold without boundary. An n-manifold is an object that looks locally like Rⁿ. In other words, every point in the space is contained in some open set that is topologically equivalent to Rⁿ. In this context, smooth means differentiable; in Rⁿ, compact means closed and bounded.

Examples: We begin with some orientable surfaces. Shown in the image below (left to right) are the sphere, the torus, and the 2-holed torus.

And now, the n-holed torus.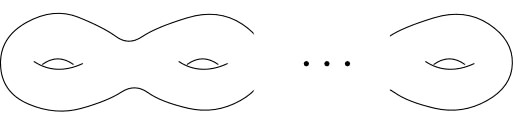

Here is another way to draw a torus.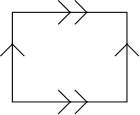

Glue along like arrows, and you'll see that it really is a torus. The point of drawing it in such a fashion (well, at least the point in this context) is that it's much easier to draw graphs on this representation of the torus than the curvy one.

The non-orientable surfaces are, of course, stranger; each has only one side. Some people like to think of this as the 'outside' flowing contiguously to the 'inside.'

The Möbius band is technically not a surface because it has a boundary.

(Such objects are called surfaces with boundary. Yes, really.)

The Klein bottle, on the other hand, has no boundary. The drawing to the right 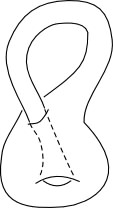appears to have a boundary at the point where the 'neck' pokes into the 'bulb.' And, it really is a boundary. (Huh?) The Klein bottle is so twisty that it can't exist in three dimensions (it's much more relaxed in a four-dimensional space) without either intersecting itself or having a boundary. It's easier for me to draw it as having a boundary than to try to figure out how to represent a self-intersection.

For further information... see this classification of surfaces page, or read the extremely excellent ZIP proof(.pdf). I'm also partial to the exposition in Massey's old GTM Algebraic Topology: An Introduction (contained, I think, in his new GTM A Basic Course in Topology) but I know, even without having looked at either of these books, that most people will prefer the newly-published Topology Now! by Messer and Straffin, or Sue Goodman's Beginning Topology.

What is an embedding?

Informal definition: An embedding is a way of drawing a graph on a surface so that none of the edges of the graph cross each other. The reason we care about embeddings is so that we can talk about faces, which are the parts of the surface that are neither edges nor vertices.

More-technical definitions: A cellular embedding is a graph drawing with no edges crossing and where the complement of the graph is composed of open topological disks. Technically, an embedding is just a particular drawing of a graph; excluding edge crossings isn't actually part of the definition, but in topological graph theory it would be rare to consider an embedding that wasn't cellular. A closed 2-cell embedding is a cellular embedding with the additional property that the closure of each face is a topological disk.

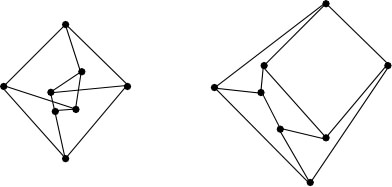
Examples: The graph below is planar, which means that it can be embedded in the sphere (or plane). It is drawn first in a non-planar way, and then it is embedded in the plane. The graph below-er is very similar, but it cannot be embedded in the plane. A drawing of this graph is paired with a toroidal embedding (an embedding of the graph on a torus).

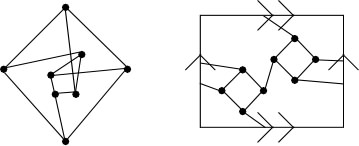
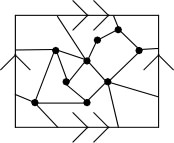
Below-left is a toroidal embedding of a graph. I'll let you figure out whether or not it can also be embedded on the sphere (in the plane). Below-right is a graph that can be embedded neither in the plane nor the torus.

For further information... on planar embeddings, check out the planarity game. After that, proceed with some caution. Almost everything written on graph embeddings assumes that the reader is a mathematician. That caveat stated, look at Wendy Myrvold's page about graph embeddings or the most-excellent monograph Graphs on Surfaces by Mohar and Thomassen, or Gross and Tucker's Topological Graph Theory.

Let's talk about edge coloring...

Informal definition: Edge coloring is a way of coloring edges. No, really, I'm not kidding, and I do mean coloring in the usual crayon-or-markers sense. Usually mathematicians implicitly mean proper edge coloring, though, which is a way of coloring edges so that no two edges that touch at a vertex have the same color.

More-technical definition: A proper edge coloring is a map f from E(G) to the set {1, ..., n}such that for any two incident edges e₁ and e₂, f(e₁) is not equal to f(e₂). (That should probably be labeled Too-technical definition...)

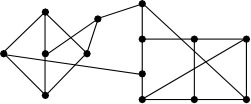
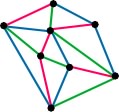
Examples: Below-left is a proper 3-edge coloring of one of the graphs shown above, and below-right is a proper 5-edge coloring of a different graph shown above. Each of these colorings is minimal, meaning that neither graph may be colored using fewer colors.

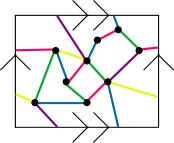
The edge coloring shown here is not proper.

On the other hand, each triangle has three different colors...hmm, that's interesting...but I digress.

For further information... see the mathworld Edge Coloring page or look in any text on graph theory (see those recommended above). Dan Archeacon discusses three-edge colorings of triangulations and edge coloring the n-cube on his Problems in Topological Graph Theory page.

...so now we can explain what a snark is...

Informal definition: A snark is a graph for which each vertex has three edges coming out of it, and that requires 4 colors be used in order to properly-edge color it.

More-technical definition: A snark is a class-two cubic graph with girth at least 5 and cyclic edge-connectivity at least 4. Every vertex in a cubic graph has degree three. By Vizing's Theorem, every graph can be properly edge colored in either Delta or Delta+1 colors, where Delta is the maximal degree of a vertex. Those graphs that need only Delta colors are considered in class one; those that require Delta+1 colors are in class two. The girth of a graph is the length of its shortest cycle. We measure cyclic edge-connectivity by the smallest number of edges that can be deleted so that the graph is disconnected but each component contains a cycle. The girth and cyclic edge-connectivity conditions are present in the definition in order to rule out degenerate and trivial examples.

Examples: The smallest snark is the Petersen graph.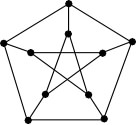

It is a graph theorist's best friend (or at least a good friend) because it's so often an excellent example or counterexample.

The next-smallest snarks are the Blanuša snarks. Neither can be embedded in the plane. One of them can be embedded on a torus; the other cannot.

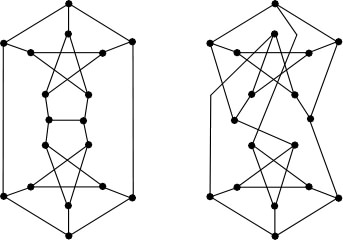
For further information... see the mathworld Snark page and One can obtain many snarks from the graph database at combinatorica.com or from Gordon Royle's cubic graphs page.

...which means that a toroidal snark is a snark that is cellularly embedded on a torus.

(This means that it has minimal genus 1, as no snark is planar, and thus that the embedding is a genus embedding.)

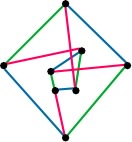
Examples: Here is the toroidal Blanuša snark.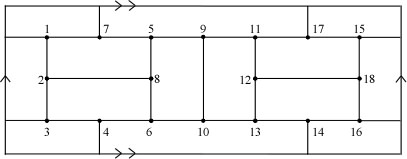

These two toroidal snarks come from a paper I wrote with Jackie Kaminski, in Graphs and Combinatorics (volume 23, number 3, June 2007, pages 229--240). They represent small members of distinct infinite families of snarks on the torus. Both families, as you might guess, are generated from the Blanuša snark above.

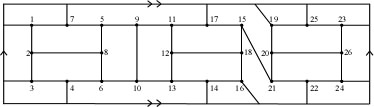
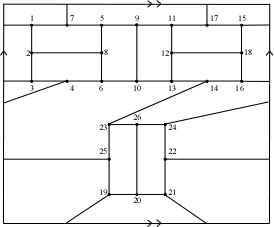
For further information... you'll have to read mathematics research papers. And if you're ready for that, you don't need any more help from this webpage...